ManiPro

Документация к ManiPro (HTML, Doxygen)
Примеры
- Линейное отображение плоскости
- Система Лоренца
Лицензия

Библиотека ManiPro предназначена для решения задачи асимптотической стабилизации по начальным данным к неподвижной точке гиперболического типа или к траектории¹.

Пусть имеется банахово пространство H, конечномерное подпространство A и непрерывное отображение S: H→H. Требуется по начальному условию a₀ найти вектор l из конечномерного подпространства A такой, что:

|Sⁿ(z₀) − Sⁿ(a₀ + l)| ≤ C qⁿ|z₀ − a₀ + l|, q < 1

При этом для отображения S должны быть выполнены условия гиперболичности². Это означает, что оператор S представим в виде суммы линейной части L и нелинейной части R. Оператор L обладает устойчивым и неустойчивым инвариантными подпространствами, прямая сумма которых дает пространство H.

Библиотека возникла как результат двухлетнего сотрудничества с Андреем Александровичем Иванчиковым по применению моего кандидатского проекта к решению задачи стабилизации с границы для задачи Навье-Стокса. Позже к проекту присоединился Андрей Алексеевич Корнев.

В результате, библиотека, которая делалась в рамках кандидатской работы, была полностью переписана на языке C, внутреннее устройство и внешний API были существенно упрощены, добавлены новые алгоритмы от Андрея Алексеевича Корнева.

Скачать manipro-2009-07-29.tar.bz2 (2,45 Mб)

Примеры

Линейное отображение плоскости

Рассмотрим отображение плоскости в себя:

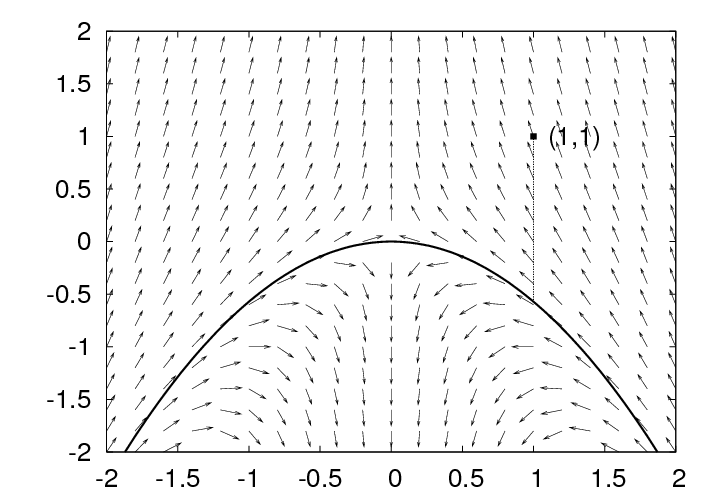
Задача состоит в том, чтобы изменить первую координату точки (y, x) так, чтобы получившаяся точка (y + a, x) стремилась к нулю под действием отображения.

Данная задача может быть решена аналитически, что может быть использовано для проверки правильности работы программы.

В данном случае задача стабилизации сводится к проектированию точки (y, x) на инвариантное устойчивое многообразие данного отображения. Инвариантное многообразие задается уравнением x = −4/7 y²:

Инвариантное устойчивое многообразие

Зададим операторы S, L, обратный к L оператор, а также скалярное произведение:

void S_step (double * h1, const double * h, int n, void * user_data)
{
    h1[0] = 2.0 * h[0] + h[1] * h[1];
    h1[1] = 0.5 * h[1];
}

void Lz_step (double * h1, const double * h, const double * z,
    int n, void * user_data)
{
    h1[0] = 2.0 * h[0];
    h1[1] = 0.5 * h[1];
}

void Lz_1_step (double * h1, const double * h, const double * z,
    int n, void * user_data)
{
    h1[0] = 1. / 2.0 * h[0];
    h1[1] = 1. / 0.5 * h[1];
}

double scalar (const double * a, const double * b, int n, void * user_data)
{
    int i;
    double sum = 0;
    for (i = 0; i < n; ++i)
    {
        sum += a[i] * b[i];
    }

    return sum;
}

Отметим, что инвариантные подпространства оператора L совпадают с осями X и Y. Настроим и вызовем алгоритм стабилизации:

    double z[2];    // неподвижная точка
    double a[2];    // заданная точка, проекция которой строится
    double aw[2];    // результат проекции точки a


    double ppbase[2]; // для хранения базиса P_+
    double pmbaseort[2]; // для хранения базиса P_-^\perp
    double kbase[2];     // для хранения базиса K

    Projector_Parameters params;

//-    По условию имеем:
    z[0] = 0.;
    z[1] = 0.;

//базис устойчивого инвариантного подпространства
    ppbase[0]    = 1.0;
    ppbase[1]    = 0.0;

//базис сопряженного к неустойчивому инвариантному подпространству
    pmbaseort[0] = 1.0;
    pmbaseort[1] = 0.0;

//базис конечномерного подпространства допустимых смещений
    kbase[0]    = 1.0;
    kbase[1]    = 0.0;


//-    Возьмем некоторую  точку из окрестности z, например:
    a[0] = 1;
    a[1] = 1;


//-    Инициализация стандартного набора параметров проектирования:
//-    означает
//-    проектирование вдоль Kbase на подпространство P_-H, являющееся
//-    приближением к W_- в точке a с точностью O(|z-a|^2),

    init_parameters (&params);

    params.steps = -1; // автоматически перевычислится,
    // по умолчанию 1

    params.levels = 1; // "типичное" значение для получения
    // "разумной" проекции
    // (приличная точность за
    // небольшие вычислительные затраты)
    // по умолчанию 0

    params.eps_eq = 1e-7;

    params.local_iterations = -1; // по умолчанию =-1;

    params.sum_iterations = -1;  // по умолчанию =-1;

    manifold_project (aw, a, z, 2, 1,
                      kbase, 1, ppbase, pmbaseort,
                      &params, S_step, Lz_step, Lz_1_step, scalar, 0);

Система Лоренца

Рассмотрим систему уравнений:

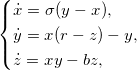
Формула № 2

Сделаем замену переменных и преобразуем систему к виду:

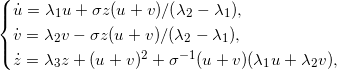
Формула № 3

Рассмотрим задачу: изменить координату v так, чтобы траектория системы с начальной точкой (u, v + l, z) стремилась к нулю. Отметим, что в данной системе координат инвариантные подпространства оператора L это плоскость X×Z и прямая Y.

Зададим операторы S, L, обратный к L оператор, а также скалярное произведение:

    struct LorenzPrm {
    double sigma;
    double r;
    double b;
    double tau;

    double l[3];
};


double Lorenz_S_rp (const double *x, int i, void * d)
{
    LorenzPrm * conf = (LorenzPrm*)d;
    double result    = 0.0;
    switch (i)
    {
    case 0:
        result = conf->l[0] * x[0]
                 + conf->sigma * x[2] * (x[0] + x[1])
                 / (conf->l[1] - conf->l[0]);
        break;
    case 1:
        result = conf->l[1] * x[1]
                 - conf->sigma * x[2] * (x[0] + x[1])
                 / (conf->l[1] - conf->l[0]);
        break;
    case 2:
        result = -conf->b * x[2] + (x[0] + x[1]) * (x[0] + x[1])
                 + 1.0 / conf->sigma * (x[0] + x[1])
                 * (conf->l[0] * x[0] + conf->l[1] * x[1]);
        break;
    default:
        printf ("Lorenz_S_rp error\n");
        exit (1);
    }
    return result;
}

double Lorenz_L_rp (const double *x, int i, void * d)
{
    LorenzPrm * conf = (LorenzPrm*)d;
    double result    = 0.0;
    switch (i)
    {
    case 0:
        result = conf->l[0] * x[0];
        break;
    case 1:
        result = conf->l[1] * x[1];
        break;
    case 2:
        result = -conf->b * x[2];
        break;
    default:
        printf ("Lorenz_L_rp error\n");
        exit (1);
    }
    return result;
}

double Lorenz_L_1_rp (const double *x, int i, void * d)
{
    return -Lorenz_L_rp (x, i, d);
}

void lorenz_init (LorenzPrm * prm, double sigma, double r, double b, double tau)
{
    prm->sigma = sigma;
    prm->r     = r;
    prm->b     = b;
    prm->tau   = tau;

    prm->l[0]  = - (sigma + 1.0) / 2.0
                 - sqrt ( (sigma + 1.0) * (sigma + 1.0) / 4.0
                 + sigma * (r - 1.0) );
    prm->l[1]  = - (sigma + 1.0) / 2.0
                 + sqrt ( (sigma + 1.0) * (sigma + 1.0) / 4.0
                 + sigma * (r - 1.0) );
    prm->l[2]  = -b;
}

void S_step(double * h1, const double * h, int n, void * user_data)
{
    LorenzPrm * prm = (LorenzPrm*)user_data;
    runge5(h1, h, n, prm->tau, Lorenz_S_rp, user_data);
}

void Lz_step(double * h1, const double * h, const double * /*z*/,
    int n, void * user_data)
{
    LorenzPrm * prm = (LorenzPrm*)user_data;
    runge5(h1, h, n, prm->tau, Lorenz_L_rp, user_data);
}

void L_1_step(double * h1, const double * h, const double * /*z*/,
    int n, void * user_data)
{
    LorenzPrm * prm = (LorenzPrm*)user_data;
    runge5(h1, h, n, prm->tau, Lorenz_L_1_rp, user_data);
}

double scalar(const double * a, const double * b, int n, void * /*user_data*/)
{
    int i;
    double sum = 0.0;
    for (i = 0; i < n; ++i) {
        sum += a[i] * b[i];
    }

    return sum;
}

Настроим и вызовем алгоритм стабилизации:

LorenzPrm prm;
double z[2];
double h0[3];
double h1[3];
double h2[3];

double ppbase[3 * 3];

double t   = 0.0;
double tau = 0.01;
double nr1 = 1e10, nr2;

int nx = 0, i;

z[0]=0.0;
z[1]=0.0;

Projector_Parameters params;

lorenz_init(&prm, 28, 10, 8. / 3., tau);

for (i = 0; i < 3; ++i) {
    if (prm.l[i] > 0) {
        //ур-я Лоренца в системе координат с диагональной правой частью
        //в l[i] i'е собственное значение
        //такой способ не будет работать при стабилизации в окрестности
        //другой точки (не нуля)
        memset(&ppbase[nx * 3], 0, 3 * sizeof(double));
        ppbase[nx * 3 + i] = 1.0;

        nx ++;
    }
}

h0[0] = h0[1] = h0[2] = 1.0;

init_parameters(&params);
params.type = 35;
params.steps = 100;
params.local_iterations = 16;

manifold_project(h1, h0, z, 3, nx,
                 ppbase, nx, ppbase, ppbase,
                 &params, S_step, Lz_step, L_1_step, scalar, &prm);

printf("x = %lf, y = %lf, z = %lf ->\n", h0[0], h0[1], h0[2]);
printf("x = %lf, y = %lf, z = %lf   \n", h1[0], h1[1], h1[2]);

//проверка сходимости к нулю
for (i = 0; i < 1000; ++i) {
    S_step(h2, h1, 3, &prm);
    nr2 = norm2(h2, h1, 3);

    if (nr2 > nr1) break;

    memcpy(h1, h2, 3 * sizeof(double));
    nr1 = nr2;
    t += tau;
}

printf("norm=%le\ttime=%le\n", nr1, t);

Результат работы алгоритма:

../bin/lorenz
steps=100
type=35
x = 1.000000, y = 1.000000, z = 1.000000 ->
x = 1.000000, y = 0.014620, z = 1.000000
norm=1.789221e-05       time=2.800000e+00

Здесь x = 1.000000, y = 1.000000, z = 1.000000 — исходная точка, x = 1.000000, y = 0.014620, z = 1.000000 — точка получившаяся в процессе стабилизации. Как можно видеть, после стабилизации траектория стремится к нулю в течении 2.8 единиц времени и приближается к нулю на расстояние 1.7×10^-5.

В указанных выше примерах инвариантные подпространства оператора L находятся аналитически. В более сложных случаях это сделать невозможно.

Для численного вычисления инвариантных подпространств ManiPro использует библиотеку arpack. Подробнее об использовании библиотеки для нахождения инвариантных подпространств вы можете узнать, рассмотрев более сложные примеры, имеющиеся в дистрибутиве ManiPro (example_05nsba и example_4-3d-L в директории src-examples).

¹ Иванчиков А. А., Корнев А. А., Озерицкий А. В. О новом подходе к решению задач асимптотической стабилизации. Поступила в редакцию ЖВМиМФ 15 мая 2009 г.

² Аносов Д. В. Геодезические потоки на замкнутых римановых многообразиях отрицательной кривизны // Труды матем. ин-та им. В. А. Стеклова. Т. 90, 1967.