Phelm

1. Phelm Documentation (HTML, Doxygen)
2. Phelm Reference Manual (PDF, 849 Кб)
3. Хранилище с исходным кодом на Bitbucket
4. Лицензия
5. Примеры
   • Уравнение Лапласа на сфере
   • Сдвоенные уравнения Лапласа в прямоугольнике
6. Благодарности

Библиотека Phelm предназначена для решения уравнений в частных производных на двумерных многообразиях.

Для решения этой задачи вам потребуется:

• построить триангуляцию многообразия;
• разбить многообразие на области;
• задать в каждой области локальную систему координат;
• задать функцию вычисления поверхностного интеграла в локальных координатах.

Дистрибутив библиотеки уже содержит построители сеток для сферических поверхностей и плоских прямоугольных областей.

Скачать phelm-1.0.1.tar.bz2 (141 Кб)

Примеры

Рассмотрим два основных аспекта работы с библиотекой: работу с неплоскими областями и с системами уравнений.

Кроме описанных ниже, в дистрибутиве библиотеки содержатся следующие примеры:

• уравнение Лапласа на плоскости;
• уравнение Чафе-Инфанта на плоскости;
• уравнение Чафе-Инфанта на сфере;
• уравнение баротропного вихря на сфере;
• двуслойная бароклинная модель атмосферы на сфере.

Уравнение Лапласа на сфере

Данный пример показывает как работать с неплоскими областями. Рассмотрим уравнение:

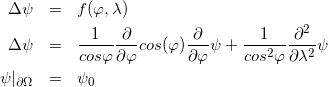
Суть метода конечных элементов состоит в том, что исходная область делится на треугольники, не имеющие общих внутренних точек. Далее, на области определяется набор базисных функций, а искомая функция ищется в виде суммы:

Базисные функции (φ_i) берут таким образом, чтобы их носитель содержал как можно меньше треугольников.

Пока библиотека Phelm поддерживает только линейные базисные функции, которые принимают значение единицы в единственном узле сетки, а в остальных узлах функция равна нулю.

Умножим скалярно уравнение на все базисные функции (их ровно столько, сколько узлов сетки):

В итоге, получим систему уравнений на значения искомой функции во внутренних узлах сетки.

Заметим, что в уравнение входят скалярные произведения между производными базисных функций (в левой части уравнения) и базисными функциями (в правой части уравнения). Соответственно, для создании матрицы системы линейных уравнений и правой части их надо посчитать.

Матрица системы линейных уравнений создается с помощью функции generate_matrix, а правая часть — с помощью функции generate_right_part. Обе функции принимают в качестве аргумента callback, который будет считать скалярные произведения между базисными функциями.

Для создания матрицы линейной системы callback будет выглядеть так:

/*
 * phi    = x - latitude
 * lambda = y - longitude
 */

/*
 * laplace = laplace1 + laplace2
 */

/*
 * laplace1 = (1 / cos phi d / d phi phi_i, cos phi d / phi phi_j)
 */
static double laplace1(const Polynom & phi_i, const Polynom & phi_j,
        const Triangle & trk, const Mesh::points_t & ps)
{
    return integrate_cos(diff(phi_i, 0) * diff(phi_j, 0), trk, ps);
}

/*
 * laplace2 = (1 / cos phi d / d lambda phi_i, 1 / cos phi d / d lambda phi_j)
 */
static double laplace2(const Polynom & phi_i, const Polynom & phi_j,
        const Triangle & trk, const Mesh::points_t & ps)
{
    return integrate_1_cos(diff(phi_i, 1) * diff(phi_j, 1), trk, ps);
}

double slaplace(const Polynom & phi_i, const Polynom & phi_j,
        const Triangle & trk, const Mesh::points_t & ps)
{
    return -(laplace1(phi_i, phi_j, trk, ps) + laplace2(phi_i, phi_j, trk, ps));
}

static double
slaplace_integrate_cb(const Polynom & phi_i,
                      const Polynom & phi_j,
                      const Triangle & trk,
                      const Mesh & m,
                      int point_i,
                      int point_j,
                      int, int,
                      void * user_data)
{
    return slaplace(phi_i, phi_j, trk, m.ps);
}

А для создания вектора правой части  — так:

struct slaplace_right_part_cb_data
{
    const double * F;
    const double * bnd;
};

static double
slaplace_right_part_cb(const Polynom & phi_i,
                       const Polynom & phi_j,
                       const Triangle & trk,
                       const Mesh & m,
                       int point_i,
                       int point_j,
                       int, int,
                       slaplace_right_part_cb_data * d)
{
    const double * F = d->F;
    double b = 0.0;

    if (m.ps_flags[point_j] == 1) {         // на границе
        int j0       = m.p2io[point_j];     // номер внешней точки
        const double * bnd = d->bnd;
        b += - bnd[j0] * laplace(phi_i, phi_j, trk, m.ps);
    } else {
        b += F[point_j] * integrate_cos(phi_i * phi_j, trk, m.ps);
    }

    return b;
}

В callback учтено то, что искомая функция известна на границе, поэтому часть скалярных произведений попадает в правую часть.

Решение системы уравнений:

Matrix laplace;
Mesh m;

[...]

generate_matrix(laplace, m, slaplace_integrate_cb, (void*)0);
slaplace_right_part_cb_data d;
d.F   = F;
d.bnd = boundary;
generate_right_part(&b[0], m_, (right_part_cb_t)(slaplace_right_part_cb), (void*)&d);
phelm::solve(answer, boundary, &b[0], laplace, m);

Полный пример смотрите в файле test_slaplace.cpp

А в чем же состоит работа с неплоской областью? Во-первых, заметим, что пользователь должен определить функцию вычисления поверхностного интеграла по треугольнику. Для сферы это уже выполнено в функции integrate_cos. Во-вторых, заметим, что уравнение на сфере имеет 3 особенности:

• особые точки на полюсах, в которых cos обращается в ноль;
• циклическая координата lambda;
• система уравнений вырождена в случае полной сферы.

Последняя проблема решается заданием краевого условия в единственной точке, например, в южном полюсе. Первые две проблемы можно решать разными способами.

Подразумевается, что вы разбиваете свое многообразие на области без особенностей. Сферу, например, можно разбить на 4 области со своей системой координат в каждой:

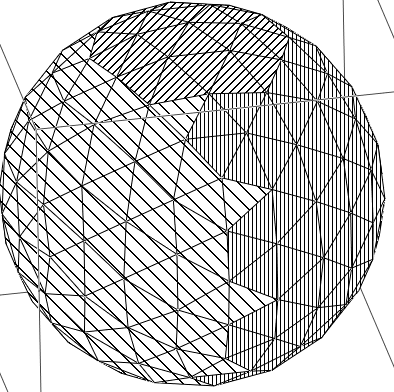
В этом случае, особых точек и циклических координат не будет.

Разбиение сферы осуществляется утилитой sphere, которая входит в дистрибутив Phelm. Использовать ее следует так:

sphere --coord local --type full --iter N > file.txt

Чем больше N, тем мельче сетка. Получившийся файл можно потом загрузить в память с помощью функции Mesh::load.

В таблице ниже представлена зависимость погрешности решения данной задачи в зависимости от размера сетки. При уменьшении шага в два раза погрешность сокращается примерно в четыре раза:

It	Число точек	Погрешность
1	41	3.03 × 10+0
2	161	6.92 × 10-1
3	641	1.39 × 10-1
4	2561	3.41 × 10-2
5	10241	7.92 × 10-3
6	40961	2.08 × 10-3
7	163841	5.87 × 10-4

Сдвоенные уравнения Лапласа в прямоугольнике

Данный пример показывает как работать с системами уравнений. Рассмотрим систему уравнений:

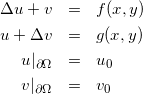
Как и в первом случае, функции u и v будем искать в виде суммы. Умножим оба уравнения системы скалярно на базисные функции и составим систему уравнений.

Пусть триангуляция, на которой решаем уравнение, состоит из N внутренних точек. Тогда размерность матрицы системы будет 2N × 2N, а размерность вектора — 2N. При этом, первые N строк матрицы относятся к первому уравнению системы, а следующие N строк — ко второму; первые N столбцов матрицы относятся к функции u, следующие N столбцов — к функции v. Аналогично с вектором правой части: первые N элементов вектора правой части относятся к первому уравнению, а следующие N элементов — ко второму.

Функции generate_matrix и generate_right_part обходят в цикле все пересекающиеся базисные функции один раз, поэтому при обходе элементов i и j надо «сказать» генераторам, что мы хотим изменить не только элемент (i, j) матрицы или элемент (i) вектора правой части, а еще и элементы (i+N, j), (i, j+N), (i+N, j+N) матрицы и элемент (i+N) вектора правой части. Для этого используются callback, которые возвращают контейнер элементов.

Создание матрицы системы:

static elements_t
laplace_integrate_cb( const Polynom & phi_i,
                      const Polynom & phi_j,
                      const Triangle & trk,
                      const Mesh & m,
                      int point_i, int point_j,
                      int i, int j,
                      void * user_data)
{
        int rs = (int)m.inner.size();
        elements_t r;
        double a;

        a = laplace(phi_i, phi_j, trk, m.ps);
        // Delta u
        r.push_back(Element(i,      j,      a));
        // Delta v
        r.push_back(Element(i + rs, j + rs, a));

        a = integrate(phi_i * phi_j, trk, m.ps);
        // v
        r.push_back(Element(i,      j + rs, a));
        // u
        r.push_back(Element(i + rs, j,      a));
        return r;
}

Здесь rs — это размерность матрицы.

Создание правой части:

struct laplace_right_part_cb_data
{
        double * F;
        double * G;

        double * BU;
        double * BV;
};

static elements_t
laplace_right_part_cb( const Polynom & phi_i,
                       const Polynom & phi_j,
                       const Triangle & trk,
                       const Mesh & m,
                       int point_i, int point_j,
                       int i, int j,
                       laplace_right_part_cb_data * d)
{
        int rs = (int)m.inner.size();
        elements_t r;
        const double * F = d->F;
        const double * G = d->G;

        if (m.ps_flags[point_j] == 1) {
                int j0       = m.p2io[point_j];
                const double * BU = d->BU;
                const double * BV = d->BV;
                double a = laplace(phi_i, phi_j, trk, m.ps);
                double b = integrate(phi_i * phi_j, trk, m.ps);

                r.push_back(Element(i,      j, -(BU[j0] * a + BV[j0] * b)));
                r.push_back(Element(i + rs, j, -(BV[j0] * a + BU[j0] * b)));
        } else {
                double a = integrate(phi_i * phi_j, trk, m.ps);
                // F
                r.push_back(Element(i,      j, F[point_j] * a));
                // G
                r.push_back(Element(i + rs, j, G[point_j] * a));
        }

        return r;
}

Отметим, что параметр j в данном случае не используется, и вместо него можно подставить все, что угодно.