SP « Проекты « Сайт Алексея Озерицкого

SP

Библиотека SP является расширением библиотеки spherepack, написанной в University Corporation for Atmospheric Research. Предоставляет удобный C++ интерфейс к spherepack, а также реализует некоторые уравнения в частных производных: уравнение Лапласа, уравнение Чафе-Инфанта, уравнение баротропного вихря и двуслойную бароклинную модель.

Используя примитивы из SP, а также генератор матрицы из реализации двуслойной бароклинной модели, пользователь библиотеки может самостоятельно реализовать практически любое уравнение или систему уравнений в частных производных на сфере.

Сборка

Для сборки библиотеки потребуется мой порт spherepack на С, а также моя библиотека linal.

Скачать sp-1.0.1.tar.bz2 (141 Кб)

Скачать linal-1.0.tar.bz2 (28 Кб)
Перейти на страницу загрузки порта Spherepack на С

Порт создан с помощью программы f2c. При генерации C-кода все переменные типа float (real) были заменены на переменные типа double, что повысило точность библиотеки. Также был написан файл spherepack.h и файл сборки CMakeLists.txt. В файле CMakeLists.txt экспортируется переменная SPHEREPACK_INCLUDE, поэтому сам spherepack_c можно использовать в своих проектах в любом месте и задавать путь к инклудникам для компилятора с помощью этой переменной.

Порядок сборки:

tar xvf sp-x.y.z.tar.bz2
cd sp
tar xvf ../linal-x.y.z.tar.bz2
tar xvf ../spherepack_c-3.2.tar.bz2
mkdir build
cd build
cmake -DCMAKE_BUILD_TYPE=Release ..
make

Примеры

Уравнение Лапласа

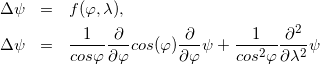
Уравнение Лапласа реализовано в файле lapl.cpp, а пример его решения — в test_lapl.cpp. lapl.cpp является оберткой над функциями slapec и islapec библиотеки spherepack.

В общем случае уравнение Лапласа на сфере имеет бесконечное число решений, поэтому функция islapec использует условие ортогональности единице при обращении оператора Лапласа.

Уравнение Чафе-Инфанта

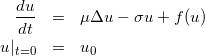
Уравнение Чафе-Инфанта реализовано в файле chafe.cpp, а пример его решения в — в test_chafe.cpp. Для аппроксимации по времени используется схема Кранка-Николсон, по пространству — функции slapec и islapec библиотеки spherepack (обернутые в lapl.cpp).

Уравнение баротропного вихря

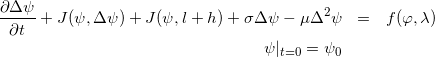
Уравнение баротропного вихря реализовано в файле barvortex.cpp, а пример его решения — в test_barvortex.cpp. Для аппроксимации по времени используется схема Кранка-Николсон. Для аппроксимации по пространству оператора Лапласа используется функция slapec библиотеки spherepack (обернутая в lapl.cpp). Для аппроксимации Якобиана используется функция gradec библиотеки spherepack (обернутая в jac.cpp).

Двуслойная бароклинная модель

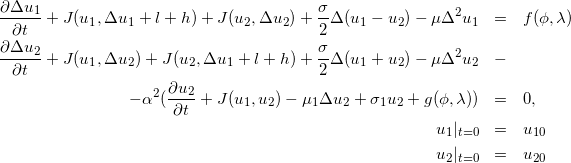
Двуслойная бароклинная модель реализована в файле baroclin.cpp, а пример его решения — в test_baroclin.cpp

Этот пример представляет наибольший интерес, так как он является системой из четырех уравнений с четырьмя неизвестными (w₁, w₂, u₁, u₂). Все предыдущие уравнения решались по такой схеме:

составяем правую часть с помощью последовательного применения операторов из spherepack;
обращаем оператор Лапласа (функция islapec).

Данный пример решается по схеме:

составляем матрицу системы уравнений;
составяем правую часть с помощью последовательного применения операторов из spherepack;
находим коэффициенты разложения правой части по сферическим гармоникам (функция shaec библиотеки spherepack, обернута в operator.cpp);
решаем систему линейных уравнений и находим коэффициенты разложения по сферическим гармоникам для w₁, w₂, u₁, u₂;
по найденным коэффициентам находим сами неизвестные w₁, w₂, u₁, u₂ (функция shsec библиотеки spherepack, обернута в operator.cpp).

Ниже приведен код построения матрицы системы линейных уравнений:

double tau   = conf.tau;
double theta = conf.theta;
double sigma = conf.sigma;
double sigma1 = conf.sigma;
double alpha = conf.alpha;
double mu    = conf.mu;
double mu1   = conf.mu1;

long nlat = conf.nlat;
long mmax = std::min (conf.nlat, conf.nlon / 2 + 1);
long n1   = 2 * conf.nlat * (std::min (conf.nlat, conf.nlon / 2 + 1) );

long i0, j0;

i0 = 0;
j0 = 0;

for (int l = 0; l < 2; ++l)
{
	for (long n = 0; n < nlat; ++n)
	{
		for (long m = 0; m < mmax; ++m)
		{
			int fnn = -n * (n + 1); // собственное значение

			// 1
			// w1
			A.add (i0, i0, 1. / tau + theta * sigma * 0.5 - theta * mu * fnn);
			// w2
			A.add (i0, i0 + n1, -theta * sigma * 0.5);

			// 2
			// w1
			A.add (i0 + n1, i0, theta * sigma * 0.5);
			// w2
			A.add (i0 + n1, i0 + n1,
				   1. / tau + theta * sigma * 0.5 - theta * mu * fnn +
				   + alpha * alpha * theta * mu1);
			// u2
			A.add (i0 + n1, i0 + 3 * n1, -alpha * alpha / tau - alpha * alpha * sigma1);

			// 3
			// Delta u1 - w1 = 0
			// w1
			A.add (i0 + 2 * n1, i0, -1);
			// u1
			A.add (i0 + 2 * n1, i0 + 2 * n1, fnn ? fnn : -1);

			// 4
			// Delta u2 - w2 = 0
			// w2
			A.add (i0 + 3 * n1, i0 + n1, -1);
			// u2
			A.add (i0 + 3 * n1, i0 + 3 * n1, fnn ? fnn : -1);

			i0 += 1;
		}
	}
}

Отметим, что построение матрицы очень похоже на аналогичное матрицы для двуслойной бароклинной модели в библиотеке phelm. Также отметим, что здесь используется условие ортогональности единице (fnn ? fnn : -1), иначе матрица окажется вырожденной.